北京市十一学校非官方网站数学谜题集

介绍

这里包含了很多的有趣的单人可尝试的数学谜题，欢迎来玩。 有些东西文字说不太清楚，自己试试就知道了 LoL
推出：BNDS OIers 信息学竞赛社，译者与发布者：@ztr 和 @xjs
此网站基于 Simon Tatham 的谜题集翻译制作
下面有 标记的是龚老师数学文化节上的数学谜题
有 标记的是我们的推荐谜题（不包含龚老师已经选择的）
Updated 2025/01/10：修改了部分谜题的名称以更符合其玩法，增加了部分内容的汉化。

谜题

黑盒
通过反射激光找出隐藏的小球

岛屿
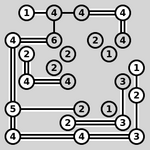用桥梁连接所有岛屿

拾色
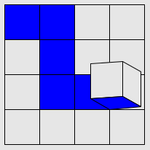通过滚动方块捡起所有涂色的格子

多米诺骨牌
用一整套多米诺骨牌填满矩形

数字华容道
通过移动小方块将数列排序

分割
用它所包含的面积标记每个方格

翻转
通过翻转若干组方块使得所有方块都被点亮

霓虹灯
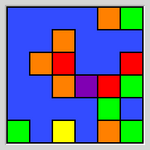通过尽可能少的改变颜色让整张图的颜色相同

对称
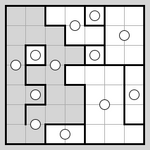将网格划分为若干个中心对称的小区域

猜色
尽可能快的找到颜色们的组合

惯性
在不滚动到炸弹上的前提下收集所有宝石

拉丁
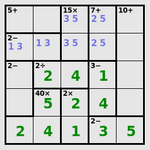通过数字提示完成拉丁方格

照亮
通过放置灯泡照亮所有方格

循环
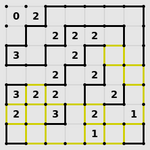在给定最大的相邻边数的前提下建立封闭图形

磁铁
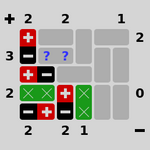放置磁铁来满足给定的条件并确保相同的磁铁不相邻

染色
恰当的给方格染色使得相邻的方格颜色不同

扫雷
在不触碰地雷的前提下找到所有地雷

黑白
在给定每个点附近黑点的数量的前提下给点染色

电路
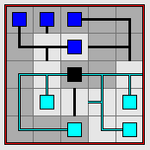旋转每个小方块来让图网重新联通

滚动
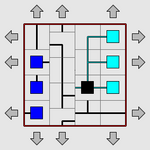通过滚动列来让图网重新联通

分割
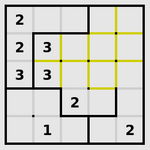在给定限制的情况下将矩阵分割为若干个面积相等的部分

图案
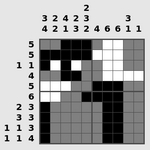在给定连续的黑色段长度的前提下给方格染色

珍珠
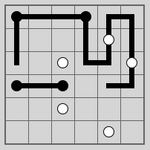在给定线段类型后绘制封闭图形

钉子
通过移动钉子移除所有的钉子

视距
放置不透明方块来限制编号格子能看到的范围

划分
将矩阵分割为若干个大小与给定数字相同的小区域

去重
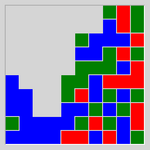通过将连续的相同数字的矩形消除移除整个矩形

路标
依据给定的路标构建从起点到终点的路径

独奏
给方格恰当的染色使得每一个行的数值都不重复

数字滑容道
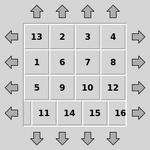通过滑动矩形将整个矩阵排序

接线
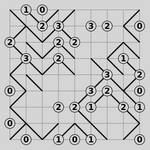在矩形上绘制斜线使得与给定的度数信息匹配

数独
恰当的填数使得每一行每一列每一个方格的数都不重复

露营
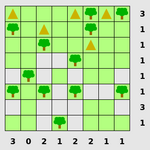在每棵树旁边放置一个帐篷

高塔
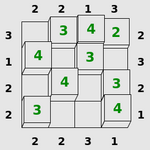根据提示数字确定高塔的高度

轨道
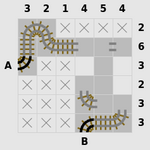根据给定的提示修建轨道

旋转
旋转小方块来将它排序

亡灵
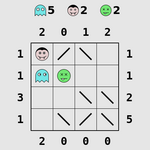恰当的放置幽灵，吸血鬼和僵尸使得在镜子中看到正确数量的幽灵

不等
通过给定的大小关系完成拉丁方块

井字棋
正确的给矩阵染色使得不存在连续的三个相同颜色的方块

解线
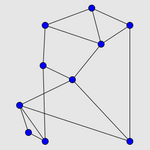修改点的位置来把节解开

版权协议